Population Genetics I: Random breeding
Ordinary genetics looks at how one selects breeding stock to produce the best possible offspring. Population genetics looks at the statistical distribution of genes in a particular breeding population, such as a breed of dog, and how different kinds of selection can affect that gene distribution. (Increasingly, population genetics also involves looking at the relationship between species by using gene sequencing as a tool.) You can think of ordinary genetics as predicting the phenotypic makup of the next generation, while population genetics predicts the genetic makeup of the breed as a whole, often several generations away.
This article is based on the assumption that the population is random breeding - an animal is equally likely to mate with any other animal in the population. This is obviously not really true - a dog in California is much more likely to mate with another California dog than with one in New York, a Great Dane is more likely to mate with another Great Dane than with a Papillion, and many breeders of domesticated animals practice deliberate breeding to relatively close relatives. We'll look at possible effects of this later on (if I get around to it). Random breeding with selection based on a single gene is the simplest case, with which other possibilities can be compared.
Unfortunately, I'll have to use a little algebra to do this. I promise I'll try to explain the results in non-mathematical terms.
We need to start by defining a few things.
A gene pool refers to the sum total of genes (and how many of each combination) found in a breeding population. The breeding population may be a single kennel that changes its gene pool every time it breeds to an outside dog, in which case the gene pool can be considered leaky, or at the other extreme may be all of the animals within a pure breed. One can speak of the gene pool of an entire species, but it is simply not true that any member of the species can mate with any other member with equal probabilty. There are species with continuous ranges where a particular gene is very rare at one end of the range and very common at the other - any member of the species can mate with any other, but by far the most likely matings are of relatively near neighbors.
We will deal with a single autosomal locus (no sex-linked genes) with a single pair of alleles, which we will call K and k. Our breeding population is made of of three different types of animals:
KK, which are genetic clears. We will call the fraction of clears in the population n, for normal.
Kk, which are carriers, meaning that they can produce affected animals. We will call the fraction of carriers in the population c, for carrier.
kk, which we will call affected, meaning that they show the effect of the k gene in double dose. We will call the fraction of affecteds in the population a, for affecteds.
Note that n + c + a = 1 = 100%, as every animal in the population is one of the three states.
Note also that "affected" can mean something as innocuous as brown rather than black pigment or something as serious as blindness, bleeding disorders or even prenatal death. I am also making no stipulation at this point as to whether the Kk state can be distinguished from KK. There are a rapidly increasing number of cases in which Kk, once distinguisable from KK only by imperfect breeding tests, can now be identified by genetic testing.
A gene frequency refers to the fraction of the genes in the breeding population that is of a particular type. The gene frequencies of all of the different alleles at a locus must add up to 100%, or 1. We are dealing with a two-allele locus (K and k) so we will define f as the frequency of the k allele and (1-f) as the frequency of the K allele. How does this relate to our clear-carrier-affected numbers?
Each dog has two genes. A fraction n is normal, and has two K genes. They contribute nothing to f. A fraction c are carriers, with one half of their genetic makeup k; they contribute c/2 to f. Finally, the affecteds contribute a to f. This gives
f = c/2 + a.
As a general rule, we do not know the value of c, as not all carriers are identified. But if we assume random breeding, the probabilities of the nine types of breedings possible (normal male to normal female, normal male to carrier female, normal male to affected female, carrier male to normal female, carrier male to carrier female, carrier male to affected female, affected male to normal female, affected male to carrier female, and affected male to affected female) can be calculated if we know c, a and n. specifically, we get these fractions:
- Normal to normal: n x n.
- Carrier to carrier: c x c.
- Affected to affected a x a
- Normal to carrier (combining the cases where the male or female is the carrier): 2 x n x c
- Normal to affected: 2 x n x a.
- Carrier to affected: 2 x c x a.
We also know the expected results of each kind of breeding:
- Normal to normal all normal.
- Carrier to carrier 25% normal, 50% carrier, 25% affected.
- Affected to affected all affected.
- Normal to carrier 50% normal, 50% carrier.
- Normal to affected all carrier.
- Carrier to affected 50% carrier, 50% affected.
If we multiply the types of offspring by the fraction of the breedings in each category, and then group the offspring by their genetic makeup, we get some surprisingly simple numbers:
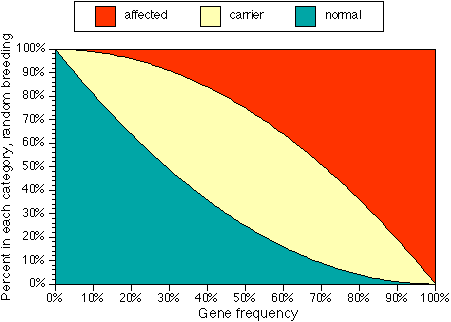
- n (fraction of normals) = (1-f) x (1 - f)
- c (fraction of carriers) = 2 x f x (1-f)
- a (fraction of affecteds) = f x f.
Figure 1. Percents of normal, carrier and affected individuals for a random-breeding population with a given gene frequency.
If we recalculate f from these values of n, c and a, it will be the same as the f we started with. Completely random breeding without selection does not change gene frequencies, unless the breeding population is so small that the assumption of a predictable distribution of types within litters of the same type or types of matings within a gene pool breaks down.
Until now we have assumed that there is no differential breeding based on whether the animal is a normal, a carrier, or an affected. Now let us assume that the kk genotype is undesirable. It does not matter whether the kk animal is a color the breeder does not like or has a lethal defect that results in its death before it reaches breeding age. For breeding purposes it is a lethal gene, i.e., all kk (affected) animals are removed from the breeding pool in each generation. For the moment we will also assume that Kk (carriers) cannot be distinguished from KK (normals.) What does this do to the frequency of the gene? (If you can't stand algebra an want to go straight to Figure 2 you can.)
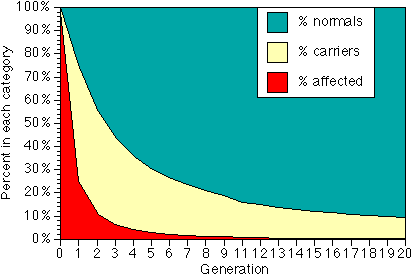
We will use subscripts (numbers below and to the right of the symbol) to indicate the generation. Thus f0 is the gene frequency in our starting generation, f1 is the is the gene frequency in the first generation after all affected animals in the initial generation are removed, f2 is the gene frequency in the next generation after the affecteds are removed, and so on. For illustrative purposes, suppose that f0 is so large that the population is effectively made up only of affecteds and carriers. After all of the affecteds are removed, however, the remaining gene pool is made up almost entirely of carriers, which by definition have a gene frequency of 50%. When these dogs are interbred, they produce 25% genetic normals, 50% carriers, and 25% affecteds, which again are discarded from the breeding pool. Our new gene pool is 2/3 carriers (f=50%) and 1/3 normals (f = 0), so f2 = 1/3. Breeding these dogs gives 1/9 affecteds, and when these are removed we have a population with equal numbers of carriers and normals, for a gene frequency of 1/4. Note that while selection solely by removing affecteds is very fast if the original percent of affecteds is high, the continued reduction after the 4th or 5th generaltion is slow.
Percent of normals, carriers and affected in each generation of a program of removing all affected animals, assuming affected condition is autosomal recessive. It doesn't show on the graph, but generation 20 would still have a quarter of a percent - one puppy in 400 - affected.
Can anything be done beyond this? Yes, provided the mode of inheritance (autosomal recessive) is known. Assume at first the carrier state cannot be distinguished from the affected state, i.e, that Kk cannot be distinguished from KK except through breeding results. (This has historically been the case with most recessive problems.) Use the breeding results to identify the carriers, and limit (not necessarily avoid at this stage) the breeding of carriers. In other words, if an animal produces affected offspring, it is a carrier and should be bred again only if it has other traits that are truly outstanding and hard to get. Full siblings of an affected animal have two chances in three of being carriers, and one in three of being normal, and these animals are less likely than the parent to produce the problem. Removing animals from the breeding pool that have produced affected animals is the next step in lowering the gene frequency.
Between test breeding and DNA sequencing, the number of conditions in which the carrier state can be unambiguously identified is increasing rapidly, and the obvious answer is not to breed carriers. However, I hesitate to recommend any breeding strategy which would remove over 10% of the gene pool due to a single gene. This could easily happen if the carrier state is identified, and has resulted in health problems in the past when the few genetic clears for one problem turned out to carry a different problem. However, there are a couple of intermediate strategies which will lower the gene frequency to the point that carriers can be eliminated safely, while at the same time minimizing the number of affecteds produced.
First, breed carriers only to tested normals. This will eliminate the production of affected offspring, but it does nothing in itself to reduce the gene frequency of the unwanted gene.
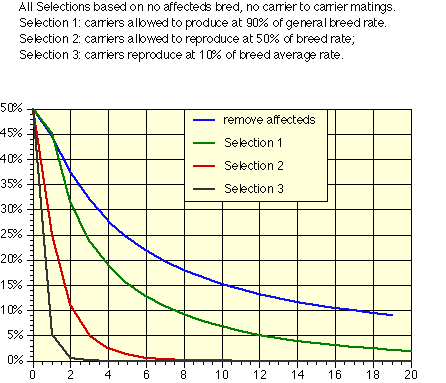
Second, treat carrier status as a fairly serious fault. The idea is to reduce the use of carriers while not eliminating them entirely until the carrier frequency drops below 5 to 10%. The figure below is based on how the carrier frequency would change with time if various percents of the carrier-normal breedings that would take place on a random basis were not made.
The point of this figure is not to select heavily against carriers, as that will result in too much loss in genetic diversity if the carrier frequency is high. Rather, it is that not making carrier to carrier breedings, while cutting down on the total number of offspring produced by carriers, is an effective means both of eliminating the production of affected animals and of reducing the gene frequency in the population. The type and severity of selection used at any given point in time should depend on both the gene frequency and the severity of the problem.
Note that the figures all relate to a population that starts with 50% gene frequency. In practice this means that even the mildest selection, that of removing affecteds, will start out by removing more than 10% of the breeding population due to a single gene. In cases where the breeding pool has a high incidence of affecteds, a different kind of selection becomes important - aimed not so much as reducing the number of affected and carrier animals as of increasing the frequency of the normal gene. Only after the gene frequency of k has been reduced by these earlier steps can the stonger selection suggested here be applied.
Genetics Index Page
sbowling@mosquitonet.comLast modified April 7, 2010